


Next:
Cognitive Science 14
Homework Set 3 Questions
-
Suppose that a random has the following probability density
function:
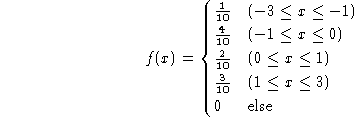
- Plot the function.
- Is the function f(x) a valid density function? Why?
In the following questions, assume f(x) is a valid density function:
- Determine the probability the variables takes on the value 2?
- Determine the probability the takes on a value between -3 and 1?
- Determine the probability the variable takes on some value?
- Is the variable continuous?
-
A carnival game uses a large wheel that is spun and then stops at a
number. Suppose that the wheel is so constructed that it can stop
at any o fthe real numbers between 0 and 6, inclusive. Suppose further
that each of these numbers has the same likelihood of occuring (that is,
the wheel is fair). Then the number where the wheel stops on any trial
is the value of a continuous random variable, the a rule given by
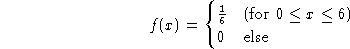
Find the following probabilities:
-
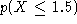
-
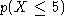
-
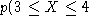
-
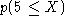
-
Using the random variable defined in problem 2:
- What is its mean,
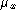 ?
?
- What is its variance,
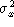 ?
?
-
A teacher believes that the class scores of a final exam are normally
distributed. If this is correct, what proportion of the class
should fall at or below the following z values?
- -1.20
- 0.96
- 1.88
- -1.78
- -0.43
- 2.15
-
A normal distribution has a mean of 500 and a standard deviation of 10.
The researcher desires to divide this distribution into five intervals
of values such that the probability of each interval will be exactly
0.20. List the desired intervals, starting with the highest.
-
A standardized test was designed so that is should produce a normal
distribution for normal adults. The testmake stated that the middle
50 % of the scores for all such adults should lie between 294 and
306. Determine the mean and standard deviation of the distribution.
-
Assume there is a discrete random variable X with the following
distribution function
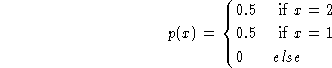
- What is the mean and the variance of this random variable.
- Imagine that we did not know the distribution of this
random variable. Instead, we only had two samples drawn from
the distribution,
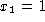 and
and 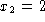 . Try to estimate
what the real values in the population are for
. Try to estimate
what the real values in the population are for 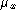 and
and
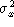 . Hint: use
. Hint: use

and that
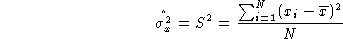
- Now assume we had drawn a different sample,
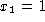 and
and 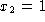 . What would be our estimates this time?
. What would be our estimates this time?
-
Now we will treat
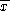 and
and 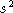 as random variables.
Each time we run an experiment and draw two samples,
as random variables.
Each time we run an experiment and draw two samples, 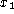 and
and
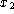 , we get a different number for
, we get a different number for 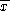 and for
and for 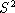 .
.
- For N=2 samples, what are all the possible values that
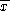 and
and 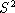 can take, and what are their probablities
... i.e. what are the distribution functions?
can take, and what are their probablities
... i.e. what are the distribution functions?
- What is the expected value for
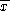 ?
?
- What is the expected value for
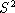 ?
?
-
Now repeat the previous problem, but use N=3.
- Is the expected value of
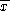 the same as
the same as
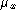 for the different N?
for the different N?
- Is the expected value of
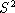 the same as
the same as
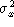 for the different N?
for the different N?
- Is there a better estimate for the population variance
than
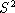 ?
?
-
A mean from a sample of 36 cases has a value of 100. How probable
is a sample mean,
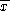 , of 100 or more when the population
is normal with the following parameters:
, of 100 or more when the population
is normal with the following parameters:
- Mean 103, standard deviation 10
- Mean 80, standard deviation 50
- Mean 99, standard deviation 4
-
Before a presidential primary in a certain state, a candidate claimed
approximately 45 % of the votes. A newspaper took a random sample of
500 voters and found 37 % would vote for him. If true value is 45 %,
how likely is it to get a sample result with 37 % or less? Do you
reject the candidates claim that he has 45 %?



Next:
Juan Miguel
Wed Aug 22 10:31:04 PDT 2001
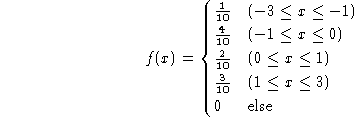
 ?
?
 ?
?
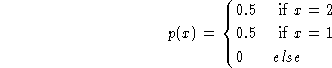
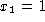 and
and 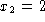 . Try to estimate
what the real values in the population are for
. Try to estimate
what the real values in the population are for 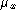 and
and
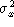 . Hint: use
. Hint: use

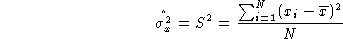
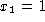 and
and 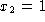 . What would be our estimates this time?
. What would be our estimates this time?
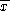 and
and 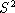 can take, and what are their probablities
... i.e. what are the distribution functions?
can take, and what are their probablities
... i.e. what are the distribution functions?
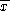 ?
?
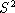 ?
?
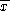 the same as
the same as
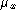 for the different N?
for the different N?
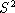 the same as
the same as
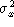 for the different N?
for the different N?
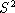 ?
?