


Next:
Cognitive Science 14
Homework Set 2 Questions
-
Suppose that a discrete random variable can take on only the values
1,2,3,4, and 5. The rule giving the probability for each of these
values is:
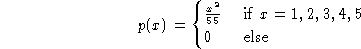
- Plot the probability mass function (distribution function).
- Determine the probability the variables takes on a value
of 2, 3, or 4?
- Determine the probability the variable takes on a value
greater than 3.5?
- Determine the probability the variable takes on some value?
- If 110 samples of the variable were taken, on average how
many would be 3's?
-
A theoretical random vairable is generated by flipping a fair coin
three times. The value of the variable is the number of heads in
three flips. What values can this variable take on, and what is
the probability of each ..... i.e., determine its distribution function.
-
Compute the mean of the random variable defined in Problem 1.
-
Compute the mean of the random variable defined in Problem 2.
-
Compute the standard deviation of the random variable in Problem 1.
-
Compute the standard deviation of the random variable in Problem 2.
-
In a test of possible side effects of a new medication, a physician
matched 20 pairs of persons on their physical characteristics. One
member of each pair was given the medicine, and the pairmate was
given a placebo. A success was recorded when the member receiving
the medication showed more of the side effect than the pairmate, and
a failure was recorded otherwise. There were 13 successes and
7 failures. If medication and placebo were equal in their tendency
to produce the effect, how likely is a result this deviate or more
deviant from what one would expect?
-
In a certain lottery, 40% of the tickets were purchased by men, and
60% by women. Each person purchased only one ticket. Ten tickets
were drawn at random and with replacement. Determine the probability
that
- Four or more winners were women.
- Two or fewer winners were women.
- The winners were all the same sex.
- Exactly four men and six women were winners.
-
A public health officer in a certain area suspects that 20% of
children in that area are severely undernourished. When a sample
of 20 children is taken at random, it is found that nine show
severe malnutrition. Determine the probability on nine or more
such children in the sample if the true proportion in the
population is 20 %. What would the officer conclude?
-
In a developemental experiment, researchers were interested in
whether newborn babies can already discriminate between colors.
To test this, they presented newborns with a green and red patch
adjacent to each other, and measured the baby's preference to
look at one or the other. The red patch appears on the right
side for half the subjects, and on the left for the other half.
If a baby looked more at the red it was counted as a 1 and
if it looked more at green as a 0. The two patches were matched
in luminosity, only differing in their color. If babies can not
see color then they should have equal chance at looking at either
patch. Twenty babies were tested, N=20, and 15 preferred red.
What is the probability we would get a result this deviant or
more deviant from the expected value if babies could not tell?
Do we have enough evidence to reject the idea babies can not
tell the difference (two-sided test)?
-
Using the same information from the baby study, assume that
researchers were instead interested in the directional hypothesis
that babies have an instinct to prefer red over green. What
is the chance we would get a value this far deviant in favor of
red if babies did not prefer either? Do we have enough evidence
to reject the idea that babies don't prefer either and instead
favor red (one-sided test)?



Next:
Juan Miguel
Mon Aug 13 17:56:54 PDT 2001